Monthly Archives: October 2018

Flow shear stabilizes rotating tokamak plasmas

Posted on by

The extremely hot plasma inside a tokamak nuclear fusion reactor ‘floats’ in a magnetic field to avoid contact with the walls. Plasma rotation has several different effects on the plasma stability, succinctly summarized in a comprehensive analytical stability criterion derived in the following publication:

Stability of localized modes in rotating tokamak plasmas
J. W. Haverkort and H. J. de Blank. Plasma Physics and Controlled Fusion, vol. 53, nr. 4, p. 045008. © 2011 DOI: 10.1088/0741-3335/53/4/045008

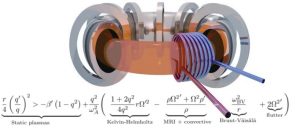
Besides well-known terms arising from the Kelvin-Helmholtz, magneto-rotational, and Rayleigh-Taylor instabilities, the criterion also contains two stabilizing terms due to rotation. One was described in an earlier post. Another less known effect was discovered to be due the Coriolis force also responsible for the circulating weather patterns in the earth atmosphere.

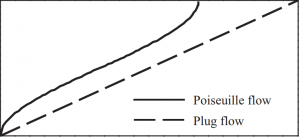
For certain conditions (See Eq. 3) the stabilizing influence of flow shear outweighs other destabilizing effects, allowing differential rotation to have a positive effect on tokamak stability.

Flow shear stabilization of rotating plasmas due to the Coriolis effect
J. W. Haverkort and H. J. de Blank. Physical Review E, vol. 86, 016411. © 2012 The American Physical Society DOI: 10.1103/PhysRevE.86.016411

Rotating tokamak plasma oscillates like atmosphere

Posted on by

Tokamak simulation

If you move an air parcel up in a quiet atmosphere its density will be higher than that of the air surrounding it so that it will fall back. The frequency of the resulting oscillation is called the Brunt–Väisälä frequency. The hot ionized plasma, inside the donut-shaped nuclear fusion tokamak, typically rotates around its central axis. The resulting centrifugal forces, similar to the effect of gravity, cause similar oscillations as in the atmosphere.

Through this effect rotation stabilizes and helps to keep the hot plasma confined. See also another post for a second positive effect of rotation.

The Brunt-Väisälä Frequency of Rotating Tokamak Plasmas
J. W. Haverkort, H. J. de Blank, and B. Koren

Journal of Computational Physics,
© 2012 DOI: 10.1016/j.jcp.2011.03.016

Doubling particle capture from laminar flow requires quadruple force

Posted on by

Particle trajectories in a parabolic and constant velocity profile

Capturing particles or droplets from a flow is relevant for various applications like continuous separators, aerosol removal, and magnetic drug targeting. In a laminar flow, doubling the capturing of a small fraction of particles turns out to require a four times higher force or length of pipe or a four times lower flow velocity (Eq. 12). This is because particles from twice as far away have to be captured from a location where the flow velocity in a laminar flow is also twice as high. This simple scaling law, with an analytical correction for flow through cylindrical pipes (Eq. 35),  turns out to hold well for a wide range of different force fields.

Magnetic particle motion in a Poiseuille flow
J. W. Haverkort, S. Kenjeres, and C. R. Kleijn

Annals of Biomedical Engineering, vol. 37, nr. 12, p. 2436-2448
© 2009 DOI: 10.1007/s10439-009-9786-y

Magnetic drug targeting possible even in large arteries

Posted on by

Movie

By attaching drugs to magnetic nanoparticles, magnetic fields can concentrate them at the location in the body where they are needed. Pre-clinical trials have shown some potential for treatment of superficial cancer tumors. More applications could be envisioned when targets deeper in the body can be reached.

Our 2009 publication was perhaps the first three-dimensional simulation showing that it is possible to capture particles from the bloodstream of large arteries like the coronary and carotid artery. This opens up the possibility of applying the technique to combat also cardiovascular diseases.

Because of an old theorem, the drugs can only be held in a stable position deep inside the body using a dynamic magnetic field configuration or in a quasi-stable position using carefully tailored magnetic fields. Despite this fundamental complication, progress remains to be made today, particularly from the perspective of computational modeling.

Computational Simulations of Magnetic Particle Capture in Arterial Flows
J. W. Haverkort, S. Kenjeres, and C. R. Kleijn

Electrical charge can be sustained in a highly conducting fluid

Posted on by

 

Magnetohydrodynamics of insulating spheres
J. W. Haverkort, T. W. J. Peeters

A widespread notion in the field of ‘ideal’ magnetohydrodynamics describing highly conducting fluids there can be no electrical charge accumulation. Any nonzero charge will quickly redistribute over a short enough time-scale to be irrelevant. One can however easily show that in the presence of a magnetic field Lorentz forces can act to sustain a finite charge density, see equation 3.  This charge and the associated electric field have a distinct influence on the current distribution and the resulting forces on non-conducting inclusions and bubbles in a conducting fluid as shown in the above picture and explained in the paper.